
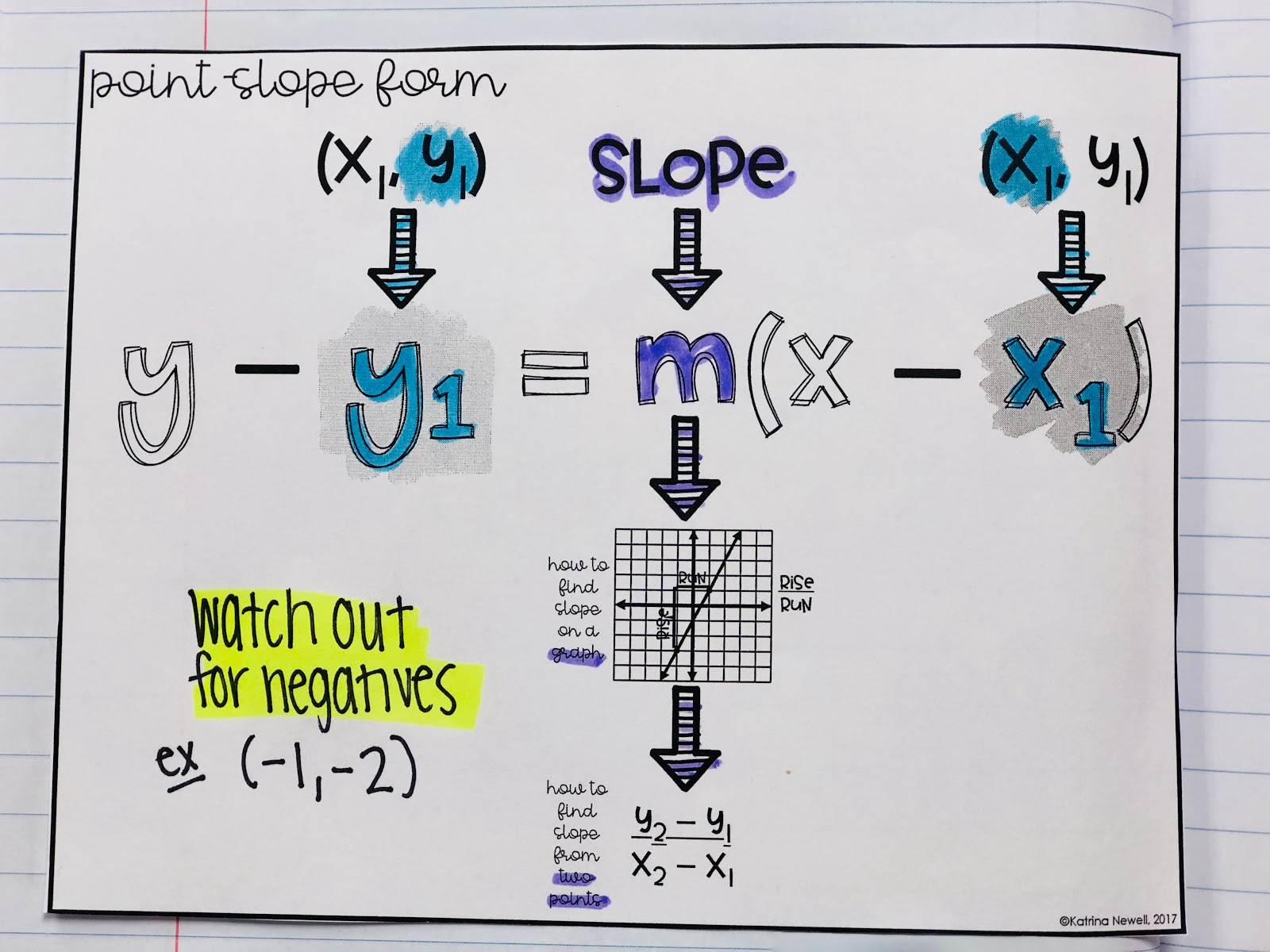
The 'point-slope' form of the equation of a straight line is:
The equation is useful when we know:
- one point on the line: (x1,y1)
- and the slope of the line: m,
and want to find other points on the line.
Write in point-slope form the equation of a line with a slope of 7 containing the point (8, 5). This is a page from the dictionary MATH SPOKEN HERE!, published in 1995 by MATHEMATICAL CONCEPTS, inc., ISBN: 0-9623593-5-1. You are hereby granted permission to make ONE printed copy of. Equation from 2 points using Point Slope Form. As explained at the top, point slope form is the easier way to go. Instead of 5 steps, you can find the line's equation in 3 steps, 2 of which are very easy and require nothing more than substitution! In fact, the only calculation, that you're going to make is for the slope. Write in point-slope form the equation of a line with a slope of 7 containing the point (8, 5). This is a page from the dictionary MATH SPOKEN HERE!, published in 1995 by MATHEMATICAL CONCEPTS, inc., ISBN: 0-9623593-5-1.
Have a play with it first (move the point, try different slopes):

Now let's discover more.

What does it stand for?
(x1, y1) is a known point

m is the slope of the line
(x, y) is any other point on the line
Making sense of it
It is based on the slope:
Slope m = change in ychange in x = y − y1x − x1
Starting with the slope: we rearrange it like this: to get this: |
So, it is just the slope formula in a different way!
Now let us see how to use it.
Example 1:
slope 'm' = 31 = 3
y − y1 = m(x − x1)
We know m, and also know that (x1, y1) = (3,2), and so we have:
That is a perfectly good answer, but we can simplify it a little:
y − 2 = 3x − 9
y = 3x − 9 + 2
y = 3x − 7
Example 2:
m = −31 = −3
y − y1 = m(x − x1)
Free slots play 999. We can pick any point for (x1, y1), so let's choose (0,0), and we have:
Point Slope Format
y − 0 = −3(x − 0)
Point Slope Form To Slope Intercept Form
Which can be simplified to:
Example 3: Vertical Line
What is the equation for a vertical line?
The slope is undefined!
In fact, this is a special case, and we use a different equation, like this:
Every point on the line has x coordinate 1.5,
that's why its equation is x = 1.5
What About y = mx + b ?

The 'point-slope' form of the equation of a straight line is:
The equation is useful when we know:
- one point on the line: (x1,y1)
- and the slope of the line: m,
and want to find other points on the line.
Write in point-slope form the equation of a line with a slope of 7 containing the point (8, 5). This is a page from the dictionary MATH SPOKEN HERE!, published in 1995 by MATHEMATICAL CONCEPTS, inc., ISBN: 0-9623593-5-1. You are hereby granted permission to make ONE printed copy of. Equation from 2 points using Point Slope Form. As explained at the top, point slope form is the easier way to go. Instead of 5 steps, you can find the line's equation in 3 steps, 2 of which are very easy and require nothing more than substitution! In fact, the only calculation, that you're going to make is for the slope. Write in point-slope form the equation of a line with a slope of 7 containing the point (8, 5). This is a page from the dictionary MATH SPOKEN HERE!, published in 1995 by MATHEMATICAL CONCEPTS, inc., ISBN: 0-9623593-5-1.
Have a play with it first (move the point, try different slopes):
Now let's discover more.
What does it stand for?
(x1, y1) is a known point
m is the slope of the line
(x, y) is any other point on the line
Making sense of it
It is based on the slope:
Slope m = change in ychange in x = y − y1x − x1
Starting with the slope: we rearrange it like this: to get this: |
So, it is just the slope formula in a different way!
Now let us see how to use it.
Example 1:
slope 'm' = 31 = 3
y − y1 = m(x − x1)
We know m, and also know that (x1, y1) = (3,2), and so we have:
That is a perfectly good answer, but we can simplify it a little:
y − 2 = 3x − 9
y = 3x − 9 + 2
y = 3x − 7
Example 2:
m = −31 = −3
y − y1 = m(x − x1)
Free slots play 999. We can pick any point for (x1, y1), so let's choose (0,0), and we have:
Point Slope Format
y − 0 = −3(x − 0)
Point Slope Form To Slope Intercept Form
Which can be simplified to:
Example 3: Vertical Line
What is the equation for a vertical line?
The slope is undefined!
In fact, this is a special case, and we use a different equation, like this:
Every point on the line has x coordinate 1.5,
that's why its equation is x = 1.5
What About y = mx + b ?
You may already be familiar with the 'y=mx+b' form (called the slope-intercept form of the equation of a line).
It is the same equation, in a different form!
The 'b' value (called the y-intercept) is where the line crosses the y-axis.
So point (x1, y1) is actually at (0, b)
and the equation becomes:
The calculator given in this section from DoMyWriting can be used to find the equation of a line when a point on the line and its slope are given.
Let (x1, y1) be a point on the line and m be the slope of the line.
Blanca ocasio cortez. Then, the formula to find the equation of a line is
y - y1 = m(x - x1)
But, the above equation can be written in the general form as shown below.
ax + by + c = 0
|
Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.
If you have any feedback about our math content, please mail us :
v4formath@gmail.com
We always appreciate your feedback.
You can also visit the following web pages on different stuff in math.
ALGEBRA Negative exponents rules COMPETITIVE EXAMS APTITUDE TESTS ONLINE ACT MATH ONLINE TEST TRANSFORMATIONS OF FUNCTIONS ORDER OF OPERATIONS WORKSHEETS | TRIGONOMETRY Trigonometric identities MENSURATION GEOMETRY COORDINATE GEOMETRY CALCULATORS MATH FOR KIDS LIFE MATHEMATICS SYMMETRY CONVERSIONS |
WORD PROBLEMS
HCF and LCM word problems
Word problems on simple equations
Word problems on linear equations
Trigonometry word problems
Word problems on mixed fractrions
OTHER TOPICS
Ratio and proportion shortcuts
Converting repeating decimals in to fractions
SBI!
